이전 포스팅에서 간략히 얘기했듯이, BIG INTEGER WITH C++를 클래스 형식으로 포팅하기로 했다.
이 코드는 벡터를 사용해서 BigInt를 구현했는데, 전체적으로 코드가 간략하다는 점이 돋보였다.
하지만, 단점이 몇 있었는데, 무엇보다도 음수를 지원하지 않는다는 점이었다.
그 외에도 로그 함수에 오류가 있었고, sqrt 함수는 성능이 너무 느렸다...
포팅을 진행하며 손을 댄 내용들을 간략히 정리해본다.
원본 코드는 stdc++.h를 사용하도록 되어있다.
이 헤더는 잡다한(?) 헤더를 몽땅 포함시키는 코드인데, 실제 상황에선 그닥 쓸모가 없다.
찾아보니 대회 같은 데 나가면 쓸만하다는데, 글쎄... 잘 모르겠다...
간략하게 쓸 내용만 추가하는 것으로 변경.
#include <iostream>
#include <vector>
#include <string>
별도의 속성을 추가했다.
0으로 나누거나, 제곱근을 잘못 처리하는 등등의 경우에 NaN으로 설정한다.
bool bMinus;
bool bInvalid;
로그 함수는 오류가 있어 통째로 변경해야 했다.
간결한 건 좋은데, 너무 간결해서 생기는 문제였다.
\(log _{31724} 471432 \approx 1.26037\cdots \) 이므로 log(31724, 471432)의 결과가 1이 나와야 하는데, 2가 나온다.
마침, 깃헙에서 훌륭한 코드를 찾았다.
이를 거의 그대로 사용해서 아래와 같은 메소드를 구성했다.
CBigInt CBigInt::log(CBigInt b, CBigInt n)
{
if (b.bInvalid || n.bInvalid || (b < 2) || (n < 1)) {
CBigInt ans;
ans.bInvalid = true;
return ans;
}
CBigInt lo(0);
CBigInt b_lo(1);
CBigInt hi(1);
CBigInt mid, b_mid;
CBigInt b_hi(b);
while (b_hi < n) {
lo = hi; b_lo = b_hi; hi = hi * 2; b_hi = b_hi * b_hi;
}
while (hi > lo + 1)
{
mid = (lo + hi) / 2;
b_mid = b_lo * pow(b, mid - lo);
if (n < b_mid) { hi = mid; b_hi = b_mid; }
if (n > b_mid) { lo = mid; b_lo = b_mid; }
if (n == b_mid) { return mid; }
}
return b_hi == n ? hi : lo;
}
제곱근 함수는 잘 동작하긴 하지만, 동작 속도가 너무 느리다.
보통 뉴턴 법이라 부르는, 근사해가며 해를 찾는 방식을 사용하는데, 커다란 숫자에선 성능이 만족스럽지 않다.
이보다는 더 빠른 방법이 많이 연구되어 있어서 이를 적용했다.
CBigInt CBigInt::sqrt(CBigInt num, const bool bRoundToNearestInt)
{
num.Set();
if (num.bInvalid || num.bMinus) {
CBigInt ans;
ans.bInvalid = true;
return ans;
}
if (IsZeroInternal(num) || (num == 1)) {
return num;
}
CBigInt res(0);
CBigInt one(1);
while (one <= num) { one *= 4; }
one /= 4; // "one" bit starts at the highest power of four <= the argument.
while (!IsZeroInternal(one)) {
if (num >= res + one) {
num = num - (res + one);
res = res + one + one;
}
res /= 2;
one /= 4;
}
/* Do arithmetic rounding to nearest integer */
if (bRoundToNearestInt && (num > res)) { ++res; }
return res;
}
이 클래스는 커다란 정수를 다루는 함수지만, 나눗셈 연산 결과를 실수 형식으로 출력하는 함수를 별도로 만들기로 했다.
프로젝트 오일러의 문제를 해결하는 과정에서 가끔 쓸 일이 있기 때문이다.
void CBigInt::printfFPdivision(CBigInt a, CBigInt b, size_t digitbelowdot, const bool printunnecessary0, const bool CRLF)
{
if (a.bInvalid || b.bInvalid || IsZeroInternal(b)) { printf("NaN"); }
else {
a.Set();
b.Set();
if (xorbool(a.bMinus, b.bMinus)) { printf("-"); }
a.bMinus = b.bMinus = false;
CBigInt n = a / b;
n.Print();
CBigInt m = a % b;
if (digitbelowdot && (!IsZeroInternal(m) || printunnecessary0)) {
printf(".");
for (size_t i = 0; (i < digitbelowdot) && (!IsZeroInternal(m) || printunnecessary0); ++i) {
m *= 10;
n = m / b;
n.Print();
m %= b;
}
}
}
if (CRLF) { printf("\n"); }
}
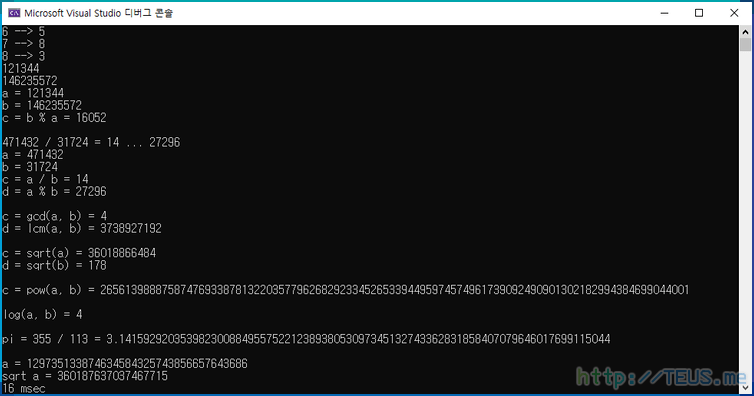
이 함수들을 실제로 적용해서 화면에 출력한 결과는 다음과 같다.
355 / 133으로 원주율을 근사하는 식의 결과를 소수점 아래 80자리까지 출력한 결과도 볼 수 있다.
참고로, 제곱근 계산에 16msec 소요된 것으로 나오는데, 제곱근 연산을 100회 반복한 결과이다.
| 집 네트워크 구성 대폭 개선 (4) | 2021.06.04 |
|---|---|
| NVMe M.2에 설치된 윈도우 시스템 복제 (5) | 2021.02.10 |
| 드디어 집에 Mesh Wi-Fi를 구축하다 (0) | 2020.11.02 |
| IEC와 EEI/IEEE의 역률(PF)의 부호 차이 (0) | 2020.10.25 |
| [MFC] CDialog vs CDialogEx (0) | 2020.10.11 |
