회사에서 뫄뫄 온도 센서의 입력값(온도)과 출력 저항값을 볼 일이 생겼다.
이 센서는 온도에 따른 출력 저항값을 한 장의 시트로 제공하는데, 대략 아래와 같은 내용이다.

이렇게 장황한 표로 뭔가를 해야되는 상황이 마음에 들지 않아 역셈을 해보기로 했다.
일단, 그래프를 그려보니 아래와 같다.

언뜻 보기에도 흔한 \(log ()\) 기반 그래프.
그래서 출력 저항값(R)에 로그를 취했다.

입력 온도와의 그래프는 아래와 같은데, 이제 뭔가 분석이란 걸 할 수 있을 것 같다.
이를 위해 추세선을 2차 함수로 그려보니 결정계수(\(R ^ 2\))가 0.9999가 나왔다.
즉, 이 추세선은 원본 데이터와 상당히 비슷하지만, 그대로 사용하기엔 무리가 있다.[각주:1]

게다가, 추세선 식을 보면 계수가 0.0001로 유효숫자가 너무 적다.
그래서 일단 로그값에 100,000을 곱해보니, 아래와 같은 결과가 나온다.

1. 2차 방정식으로 계산
출력값을 적절한 값(25℃)에서 잘라서 두 개의 추세선 식(2차 방정식)을 추출해봤다.
한 쪽 범위에서는 \(y = 17.525 x ^ 2 - 5142.7 x + 348594\) 가 나왔다.
즉, \(17.525 x ^ 2 - 5142.7 x + 348594 - 100000 log _e R = 0\)을 풀면 된다.

다른 하나의 범위에서는, \(9.525 x ^ 2 - 4779 x + 343192 - 100000 log _e R = 0\)을 풀면 된다.

두 경우 모두 상수항만 변수이고, \(x\), \(x^2\)의 계수가 상수값이므로 근의 공식에 대입하면 손쉽게 역셈할 수 있다.
간단하게 코드로 만들어보면 아래와 같다.
double CalcT(double R) {
const double lnR_100000 = 100000 * log(R);
double a, b, c;
if (lnR_100000 > 220000) {
a = 17.525;
b = -5142.7;
c = 348594 - lnR_100000;
} else {
a = 9.525;
b = -4779;
c = 343192 - lnR_100000;
}
return (-b - sqrt(b * b - 4 * a * c)) * 0.5 / a;
}
원래의 온도와 역셈한 온도값을 비교해보면 아래 처럼 깔끔하게 나온다.
파란선은 두 값의 오차를 표시한 선인데, 경계 부근에서 튀는 게 살짝 보인다.
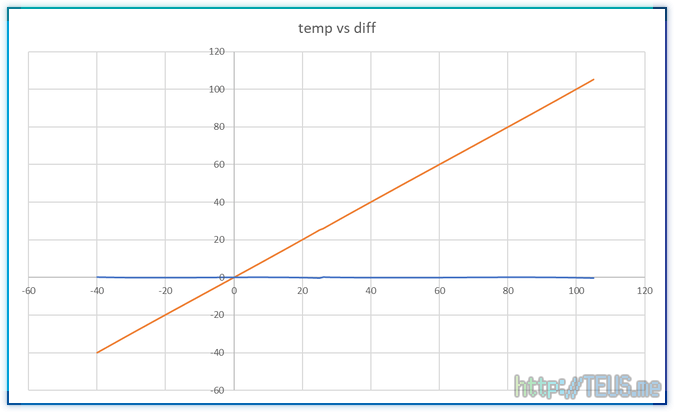
오차만 확대하면 아래와 같다.
오차의 최댓값은 0.126, 최솟값은 -0.188 정도다.

2. 3차 방정식으로 계산
추세선 식을 3차식으로 표현하면 일단 결정계수가 1로 나온다.
즉, 저 간단한(응?) 3차 방정식의 해만 구하면 식 하나로 해결이 가능한 것이다.
즉, \(-0.0351 x ^ 3 + 16 x ^ 2 - 5138.1 x + 348990 - 100000 log _e R = 0\)을 풀면 된다.

일찌기 라그랑주 선생님께서 3차 방정식의 해법을 정리해주셨고, 여기선 특히 실근만을 쓰기 때문에 손쉽게 풀 수 있다.
일단 코드로 작성하면 아래와 같다.
double CalcT(double R) {
const double lnR_100000 = 100000 * log(R);
const static double a = -0.0351;
const static double b = 16;
const static double c = -5138.1;
const double d = 348990 - lnR_100000;
const double p = -2 * b * b * b + 9 * a * b * c - 27 * a * a * d;
const double q = b * b - 3 * a * c;
const double m3 = (p - sqrt(p * p - 4 * q * q * q)) * 0.5;
const double n3 = (p + sqrt(p * p - 4 * q * q * q)) * 0.5;
const double m = -pow((-m3), 1 / 3.0);
const double n = pow(n3, 1 / 3.0);
return (-b + m + n) / 3 / a;
}
그런데, 이 코드에선 상수로 정리 가능한 불필요한 변수가 많이 사용되었다.
이를 정리하면 아래와 같다.
double CalcT(double R) {
const double lnR_100000 = 100000 * log(R);
const double d = 348990 - lnR_100000;
const double p = 17778.01264 - 0.03326427 * d;
const double m3 = (p - sqrt(p * p - 92637375.18)) * 0.5;
const double n3 = (p + sqrt(p * p - 92637375.18)) * 0.5;
const double m = -pow((-m3), 1 / 3.0);
const double n = pow(n3, 1 / 3.0);
return (-16 + m + n) * (-9.496676163);
}
원래의 온도와 역셈한 온도값을 비교해보면 아래 처럼 깔끔하게 나온다.
두 값의 오차를 표시한 파란 선도 튀는 것이 보이지 않는다.

오차만 확대하면 아래와 같다.
오차의 최댓값은 0.089, 최솟값은 -0.215 정도다.
2차 방정식으로 풀었을 때랑 비교하면 튀는 구간이 없다는 점 외에는 대동소이하고, 오차 범위도 유사하다.

3. 생각의 전환 + 4차 방정식 추세선으로 계산
앞의 해법들은 T → R의 식을 추정한 뒤, 이에 대한 해를 구해서 원래의 T 값을 계산하는 방식이었다.
이 방향을 좀 비틀어서 R → T의 식을 바로 추정해보기로 했다.
앞의 방식들에서는 100,000을 곱했는데, 이 부분이 필요가 없으며, 추세선 식은 4차 방정식으로 지정했다.

코드로 표현하면 아래와 같다.
해를 따로 구할 필요가 없어 간단하게 기술이 가능하다.
double CalcT(double R) {
const double lnR = log(R);
const double lnR2 = lnR * lnR;
const double lnR3 = lnR2 * lnR;
const double lnR4 = lnR3 * lnR;
return 0.0085 * lnR4 - 0.191 * lnR3 + 2.5613 * lnR2 - 31.887 * lnR + 86.932;
}
원래의 온도와 역셈한 온도값을 비교해보면 아래 처럼 깔끔하게 나온다.
두 값의 오차를 표시한 파란 선도 역시 튀는 것이 보이지 않는다.

오차만 확대하면 아래와 같다.
오차의 최댓값은 0.034, 최솟값은 -0.033 정도로, 앞의 방식들보다 월등히 적다.

결론1. 3번 쓰세요
결론2. 엑셀 킹왕짱 우왕ㅋ굳ㅋ
| 간략 근황 소개(LG 노트북에 탑재될뻔한 구라 제거기 등) (0) | 2020.04.12 |
|---|---|
| 업무 환경 시놀로지 적용기(시놀로지 드라이브, DB, WebDAV) (0) | 2020.04.12 |
| ASUS VivoBook D712DA-AU071 17인치 리뷰 (0) | 2019.12.22 |
| PC 전원 버튼 수리(?) (0) | 2019.12.09 |
| LCD용 고정폭 폰트 관련 삽질기 (0) | 2019.11.24 |
