n/φ(n)이 최대가 되는 백만 이하의 n은?

IT/알고리즘
2021. 7. 14. 20:19
 
 
반응형

 

그간 도저히 포스팅할 시간이 나지 않았다. 정말이지 오랜만의 포스팅.

오랜만에 오일러 프로젝트를 하나 풀어봤다.

 

오일러의 \( \phi(n) \) 함수는 주어진 숫자보다 작은 수 중에 서로소인 수의 개수이다.

수학 쪽 분들께는 아래와 같이 정의될 수 있다고 한다.

 

\( \phi(n) = n {\prod _{p|n}^{}} \left (1- \frac{1}{p} \right ) \)

 

그리고, 저 정의를 활용하면 \( n / \phi(n) \)가 최대가 되는 경우를 좀 더 손쉽게 알 수 있다고 한다.

 

그런데, 저 식을 제대로 이해하지 못하면서 코드를 만들고 싶지는 않아서 그냥 정공법으로 풀어보기로 했다.

 

첫번째 시도

모든 것을 무식하게 돌려보기로 했다.

백만 이하의 모든 수 각각에 대해 그 이하의 모든 수들과 비교해서 서로소인지를 비교.

서로소인지의 확인을 조금은 깔끔하게 하기 위해 백만 이하의 모든 수에 대한 소인수 테이블을 먼저 만들었다.

이렇게 만들 때는 에라토스테네스의 체가 큰 도움이 된다.

 

다음으로 이 테이블을 활용하여 두 수가 서로소인지 확인하는 함수를 작성.

이후는 무한히 뺑뺑이를 돈다...

그러니까 사실상 백만(Mega) × 백만(Mega) 개니까 1조(Tera)회의 루프를 도는 것...

 

너무나 오래 걸려서 결국 더 기다리지 못하고 GG 선언.

 

#include <iostream>
#include <vector>
using namespace std;

#include <Windows.h>

typedef vector<size_t> v1num_t, * pv1num_t;
typedef vector<v1num_t> v2num_t, * pv2num_t;

const static size_t MAXNUM = 1000000;

//에라토스테스트의 체를 응용한 소인수 테이블 작성
void CreatePrimeDivisorsTable(v2num_t &v, const size_t max) {
    v.clear();
    v.resize(max + 1);
    
    for (size_t i = 2; i <= max; ++i) {
        if (v[i].empty()) {
            for (size_t n = i * 2; n <= max; n += i) {
                v[n].push_back(i);
            }
        }
    }
}

bool AreRelativelyPrime(const v2num_t& v, const size_t n1, const size_t n2) {
    if (n1 == n2) {
        return false;
    }

    if (n1 == 0 || n1 == 1 || n2 == 0 || n2 == 1) {
        return true;
    }

    if ((n1 % n2 == 0) || (n2 % n1 == 0)) {
        return false;
    }

    //범위가 이상하면 서로소라고 우김
    const size_t count = v.size();
    if (n1 >= count || n2 >= count) {
        return true;
    }

    pv1num_t p1 = (pv1num_t) & (v[n1]);
    pv1num_t p2 = (pv1num_t) & (v[n2]);

    const size_t count1 = p1->size();
    const size_t count2 = p2->size();
    if (!count1 || !count2) {
        return true;
    }

    size_t po1 = 0;
    size_t po2 = 0;
    //여기까지 왔으면 서로 다른 2 이상의 두 값이
    //한 쪽이 다른 한 쪽의 약수가 아님
    //소인수 중에 일치하는 것이 있으면 서로소가 아님

    while (po1 < count1 && po2 < count2) {
        const size_t nn1 = (*p1)[po1];
        const size_t nn2 = (*p2)[po2];

        if (nn1 == nn2) {
            //공통 소인수 발견
            //서로소가 아님
            return false;
        }
        else if (nn1 < nn2) {
            ++po1;
        }
        else {
            ++po2;
        }
    }

    //끝까지 못 찾으면 서로소가 아님
    return true;
}


int main()
{
    DWORD64 dw0 = GetTickCount64();

    v2num_t vTable;
    CreatePrimeDivisorsTable(vTable, MAXNUM);

    DWORD64 dw1 = GetTickCount64() - dw0;
    dw0 = GetTickCount64();

    cout << "table created (" << dw1 << " ms)" << endl;

    double max_n_phi = 0;
    size_t max_n = 0;
    size_t max_phi = 0;

    for (size_t n = 2; n <= MAXNUM; ++n) {

        if (!(n % 1000)) {
            dw1 = GetTickCount64() - dw0;
            cout << "processing " << n << "... (" << dw1 << " ms)" << endl;
        }

        size_t phi = 0;
        for (size_t j = 1; j < n; ++j) {
            if (AreRelativelyPrime(vTable, n, j)) {
                ++phi;
            }
        }
        const double n_phi = (double)n / phi;
        if (n_phi > max_n_phi) {
            max_n_phi = n_phi;
            max_n = n;
            max_phi = phi;
        }
    }

    cout << max_n << " / phi = " << max_phi << " / " << max_n_phi << endl;
    
    dw1 = GetTickCount64() - dw0;
    cout << "finished (" << dw1 << " ms)" << endl;
}

 

두번째 시도

이건 좀 아닌 것 같아 고민을 해보니 주어진 수와 서로소인 수의 개수를 세는 건 좀 더 최적화가 가능하다.

모든 두 수를 직접 비교할 필요까지는 없는 것 같다.

주어진 수의 소인수들의 모든 배수를 표시한 뒤 표시되지 않은 수의 개수만 세면 되는 것이다.

 

표시를 중복되지 않도록만 유의하면[각주:1] 좀 더 간단히 개수를 셀 수 있다.

 

#include <iostream>
#include <vector>
using namespace std;

#include <Windows.h>

typedef vector<size_t> v1num_t, * pv1num_t;
typedef vector<v1num_t> v2num_t, * pv2num_t;

const static size_t MAXNUM = 1000000;

vector <BYTE> vTables(MAXNUM + 1);

//에라토스테스트의 체를 응용한 소인수 테이블 작성
void CreatePrimeDivisorsTable(v2num_t& v, const size_t max) {
    v.clear();
    v.resize(max + 1);

    for (size_t i = 2; i <= max; ++i) {
        if (v[i].empty()) {
            for (size_t n = i * 2; n <= max; n += i) {
                v[n].push_back(i);
            }
        }
    }
}

size_t CountRelativelyPrimes(const v2num_t& v, const size_t n) {
    //n보다 작은 숫자(1..n-1)에 대해
    //n의 소인수들의 배수들을 몽땅 마킹한 뒤
    //마킹되지 않는 숫자의 개수를 세는 거임

    size_t ret = n - 1;
    const pv1num_t p = (pv1num_t) & (v[n]);
    const size_t count = p->size();

    //소수인 경우 작업 불필요
    if (count == 0) {
        ;   //do nothing;
    }
    else {
        //테이블을 0으로 초기화
        //이 값이 0이면 서로소인 숫자
        //즉, 소인수의 배수라면 0이 아닌 값으로 변경함
        BYTE* pvTables = &(vTables[0]);
        memset(pvTables, 0, vTables.size());

        const size_t* p0 = &((*p)[0]);
        for (size_t i = 0; i < count; ++i) {
            //p0[i]의 배수들을 지워나감
            //이미 지워진 경우는 지우지 않음
            for (size_t j = p0[i]; j < n; j += p0[i]) {
                if (!pvTables[j]) {
                    pvTables[j] = 1;
                    --ret;
                }
            }
        }
    }

    return ret;
}


int main()
{
    DWORD64 dw0 = GetTickCount64();

    v2num_t vTable;
    CreatePrimeDivisorsTable(vTable, MAXNUM);

    DWORD64 dw1 = GetTickCount64() - dw0;
    dw0 = GetTickCount64();

    cout << "table created (" << dw1 << " ms)" << endl;

    double max_n_phi = 0;
    size_t max_n = 0;
    size_t max_phi = 0;

    for (size_t n = 2; n <= MAXNUM; ++n) {

        if (!(n % 50000)) {
            dw1 = GetTickCount64() - dw0;
            cout << "processing " << n << "... (" << dw1 << " ms)" << endl;
        }

        const size_t phi = CountRelativelyPrimes(vTable, n);

        const double n_phi = (double)n / phi;
        if (n_phi > max_n_phi) {
            max_n_phi = n_phi;
            max_n = n;
            max_phi = phi;
        }
    }

    cout << max_n << " / phi = " << max_phi << " / " << max_n_phi << endl;

    dw1 = GetTickCount64() - dw0;
    cout << "finished (" << dw1 << " ms)" << endl;
}

드디어! 대략 4분(240초)만에 원하는 답이 나왔다. ㅠㅠ

 

최종 시도

그런데, 생각을 더 해보니 소인수들의 배수를 일일이 확인하는 것보다는 좀 더 심플하게 개수를 셀 수 있다.

 

주어진 숫자를 어떤 소인수로 나눈 몫이 바로 그 숫자 이하에서 그 소인수의 배수의 개수가 된다.

예컨데, 17 이하의 숫자 중 3의 배수의 개수는 17 ÷ 3 = 5 … 2 이므로 5개[각주:2]가 된다.

즉, 27 이하의 숫자 중 27과 서로소인 수는 27 ÷ 3 = 9 이므로 27 - 9 = 18 개가 되는 것이다.

 

 

소인수가 둘 이상인 경우는 각 소인수의 배수들의 개수를 뺀 뒤 다시 최소공배수의 개수를 더하면 된다.

24 이하의 숫자 중 24와 서로소인 수는 24 ÷ 2 = 12, 24 ÷ 3 = 8, 24 ÷ 6 = 4 이므로 24 - 12 - 8 + 4 = 8 개[각주:3]가 된다.

 

소인수가 몇 개가 되든 인수들의 곱 테이블만 만들면 간단하게 개수를 셀 수 있지만, 문제가 있다.

모든 소인수의 곱이 64비트 범위를 벗어나면 정상적으로 동작하지 않게 된다.

1,000,000의 제곱근이 1,000 이므로 소인수가 6개 이하인 경우에만 이 개념을 적용하면 안전하게 처리가 가능하다.

 

#include <iostream>
#include <vector>
using namespace std;

#include <Windows.h>

typedef vector<size_t> v1num_t, * pv1num_t;
typedef vector<v1num_t> v2num_t, * pv2num_t;

const static size_t MAXNUM = 1000000;

vector <BYTE> vTables(MAXNUM + 1);

//에라토스테스트의 체를 응용한 소인수 테이블 작성
void CreatePrimeDivisorsTable(v2num_t& v, const size_t max) {
    v.clear();
    v.resize(max + 1);

    for (size_t i = 2; i <= max; ++i) {
        if (v[i].empty()) {
            for (size_t n = i * 2; n <= max; n += i) {
                v[n].push_back(i);
            }
        }
    }
}

//벡터에 들어있는 소인수들 2개 이상의 모든 곱을 조합해서 생성하는 함수
//소인수들의 개수가 20개 이하일 때만 사용할 것
//2개 이상의 모든 조합의 개수가 2 ^ n - 1 - n 개인데
//16개라면 65519 개의 벡터를 만들어야 함
//20개라면 2 ^ 20 - 1 - 20 = 1024 * 1024 - 21 = 1048555 개
//여기서는 6개 이하만 하기로 함
//만들어지는 곱이 비트를 넘어가면 안 되기 때문
bool CreatePrimeMulTable(const v1num_t &v, v1num_t &vMul) {
    vMul.clear();
    const size_t count = v.size();
    if (count < 2) {
        return true;
    }
    const size_t* p = &(v[0]);
    if (count == 2) {
        vMul.push_back(p[0] * p[1]);
        return true;
    }
    else if (count > 6) {
        return false;
    }

    //간단하게 0..2^n-1 까지 루프를 돌려
    //각 비트를 순서대로 소인수에 대응시키면 됨
    //이 때 1인 비트가 2개 이상일 때만 처리해야 함
    //따라서 3부터 루프를 시작하면 됨
    const size_t countb = ((size_t)1 << count);
    for (size_t i = 3; i < countb; ++i) {
        size_t countb0 = 0; //실제 곱하기를 한 횟수, 별도로 비트 카운트를 세는 intrinsic을 안 쓰고 이걸로 때움
        size_t digit = 0;
        size_t i0 = i;
        size_t mul = 1;
        while (i0) {
            if (i0 & 1) {
                mul *= p[digit];
                ++countb0;
            }
            i0 >>= 1;
            ++digit;
        }

        if (countb0 > 1) {
            vMul.push_back(mul);
        }
    }

    return true;
}

size_t CountRelativelyPrimes(const v2num_t& v, const size_t n) {
    //n보다 작은 숫자(1..n-1)에 대해
    //n의 소인수들의 배수들을 몽땅 마킹한 뒤
    //마킹되지 않는 숫자의 개수를 세는 거임

    size_t ret = n - 1;
    const pv1num_t p = (pv1num_t) & (v[n]);
    const size_t count = p->size();

    //소수인 경우 작업 불필요
    //약수가 1개인 경우 복잡하게 할 거 없이 나누기 한번으로 정리됨
    //약수가 2개까지는 코드로 최적화 가능함
    if (count == 0) {
        ;   //do nothing;
    }
    else if (count == 1) {
        ret -= (ret / (*p)[0]);
    }
    else if (count == 2) {
        ret += ((n - 1) / ((*p)[0] * (*p)[1]));
        ret -= ((n - 1) / (*p)[0]);
        ret -= ((n - 1) / (*p)[1]);
    }
    else if (count < 7) {
        v1num_t vMul;
        CreatePrimeMulTable(v[n], vMul);
        const size_t sz = vMul.size();
        if (sz) {
            size_t* pMul = &(vMul[0]);
            for (size_t i = 0; i < sz; ++i) {
                ret += (n - 1) / pMul[i];
            }
        }

        for (size_t i = 0; i < count; ++i) {
            ret += (n - 1) / ((*p)[i]);
        }
    }
    else {
        //테이블을 0으로 초기화
        //이 값이 0이면 서로소인 숫자
        //즉, 소인수의 배수라면 0이 아닌 값으로 변경함
        BYTE* pvTables = &(vTables[0]);
        memset(pvTables, 0, vTables.size());

        const size_t* p0 = &((*p)[0]);
        for (size_t i = 0; i < count; ++i) {
            //p0[i]의 배수들을 지워나감
            //이미 지워진 경우는 지우지 않음
            for (size_t j = p0[i]; j < n; j += p0[i]) {
                if (!pvTables[j]) {
                    pvTables[j] = 1;
                    --ret;
                }
            }
        }
    }

    return ret;
}


int main()
{
    DWORD64 dw0 = GetTickCount64();

    v2num_t vTable;
    CreatePrimeDivisorsTable(vTable, MAXNUM);

    DWORD64 dw1 = GetTickCount64() - dw0;
    dw0 = GetTickCount64();

    cout << "table created (" << dw1 << " ms)" << endl;

    double max_n_phi = 0;
    size_t max_n = 0;
    size_t max_phi = 0;

    for (size_t n = 2; n <= MAXNUM; ++n) {

        if (!(n % 50000)) {
            dw1 = GetTickCount64() - dw0;
            cout << "processing " << n << "... (" << dw1 << " ms)" << endl;
        }

        const size_t phi = CountRelativelyPrimes(vTable, n);

        const double n_phi = (double)n / phi;
        if (n_phi > max_n_phi) {
            max_n_phi = n_phi;
            max_n = n;
            max_phi = phi;
        }
    }

    cout << max_n << " / phi = " << max_phi << " / " << max_n_phi << endl;

    dw1 = GetTickCount64() - dw0;
    cout << "finished (" << dw1 << " ms)" << endl;
}

총 연산 시간이 1초 이내[각주:4]로 들어왔으며, 당연히 정상적인 답이 도출이 되었다.

 

진짜 최종시도

오일러의 \( \phi(n) \) 함수의 정의를 조금 공부해보니 전혀 어려운 내용이 아니었다.

(앞에서도 적었듯이) 역시 위대하신 오일러님께서 모두 다 쉽게 정리해두셨다.

 

\( \phi(n) = n {\prod _{p|n}^{}} \left (1- \frac{1}{p} \right ) \)

 

이를 적용해서 복잡한 코드들을 다 걷어내고 간단하게 수정했다.

 

#include <iostream>
#include <vector>
using namespace std;

#include <Windows.h>

typedef vector<size_t> v1num_t, * pv1num_t;
typedef vector<v1num_t> v2num_t, * pv2num_t;

const static size_t MAXNUM = 1000000;

vector <BYTE> vTables(MAXNUM + 1);

//에라토스테스트의 체를 응용한 소인수 테이블 작성
void CreatePrimeDivisorsTable(v2num_t& v, const size_t max) {
    v.clear();
    v.resize(max + 1);

    for (size_t i = 2; i <= max; ++i) {
        if (v[i].empty()) {
            //i가 소수인 경우
            for (size_t n = i * 2; n <= max; n += i) {
                v[n].push_back(i);
            }
        }
    }
}

size_t CountRelativelyPrimes(const v2num_t& v, const size_t n) {
    size_t ret = n;
    const pv1num_t p = (pv1num_t) & (v[n]);
    const size_t count = p->size();

    if (!count) {
        return n - 1;
    }

    for (size_t i = 0; i < count; ++i) {
        ret = ret * ((*p)[i] - 1) / (*p)[i];
    }
    
    return ret;
}


int main()
{
    DWORD64 dw0 = GetTickCount64();

    v2num_t vTable;
    CreatePrimeDivisorsTable(vTable, MAXNUM);

    DWORD64 dw1 = GetTickCount64() - dw0;
    dw0 = GetTickCount64();

    cout << "table created (" << dw1 << " ms)" << endl;

    double max_n_phi = 0;
    size_t max_n = 0;
    size_t max_phi = 0;

    for (size_t n = 2; n <= MAXNUM; ++n) {

        if (!(n % 50000)) {
            dw1 = GetTickCount64() - dw0;
            cout << "processing " << n << "... (" << dw1 << " ms)" << endl;
        }

        const size_t phi = CountRelativelyPrimes(vTable, n);

        const double n_phi = (double)n / phi;
        if (n_phi > max_n_phi) {
            max_n_phi = n_phi;
            max_n = n;
            max_phi = phi;
        }
    }

    cout << max_n << " / phi = " << max_phi << " / " << max_n_phi << endl;

    dw1 = GetTickCount64() - dw0;
    cout << "finished (" << dw1 << " ms)" << endl;
}

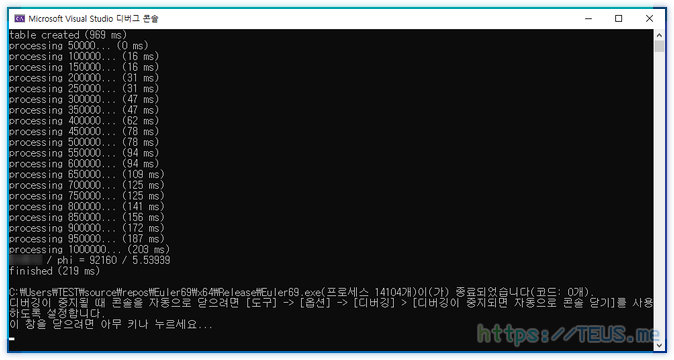
물론 결과는 동일하며, 이제 연산 자체를 200ms 정도에 끝낼 수 있었다.

맨 앞에 소인수 테이블을 만드는데 시간이 약간 걸리긴 했지만.

 

“Read Euler, read Euler, he is the master of us all.”

— Pierre-Simon Laplace

"오일러를 읽어라, 오일러를 또 읽어라. 그는 우리 모두의 스승이시다"

— 라플라스 후작[각주:5]

 

 

  1. 예컨데, 6이라면 2의 배수에서 표시가 되었으니 3의 배수에서는 표시 불필요 [본문으로]
  2. 3, 6, 9, 12, 15 [본문으로]
  3. 1, 5, 7, 11, 13, 17, 19, 23 [본문으로]
  4. 무려 노트북용 2세대 i5 CPU 환경임 [본문으로]
  5. 맞다. 모든 공돌이들의 공공의 적, 라플라스 변환의 바로 그 라플라스다. [본문으로]
반응형
저작자표시 비영리 동일조건

'IT > 알고리즘' 카테고리의 다른 글

최대공약수(GCD)를 구하는 가장 빠른 방법은?  (0) 2021.08.22
n/φ(n)이 최소가 되며 두 값이 순열관계인 천만 이하의 n은?  (0) 2021.07.14
C언어에서의 HEX2DEC() 함수 최적화  (2) 2021.01.16
음수의 나누기/나머지는 대체 어떻게 해야 되는 걸까?  (0) 2020.11.15
e의 연분수 전개시 특정 수렴값의 분자의 합  (0) 2020.11.08

공유하기

facebook twitter kakaoTalk kakaostory naver band

'IT/알고리즘' 의 관련글

티스토리툴바