ln(), pow(), exp() 함수 구현 / 마무리

앞 포스팅들을 다시 읽어보니 뭔가 마무리가 되지 않은 느낌이 들었다.

pow() 함수가 없기 때문인 것 같아서 이것까지 마저 만들기로 했다.

 

이미 ln()과 exp() 함수가 있기 때문에 구현 자체는 어려운 게 없다.

아래 적힌 관계만 이용하면 된다.

 

 

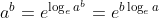
여기서 유의해야 될 점은 몇 가지 예외조건이 있다는 것이다.

이런 점을 고려한 코드는 아래와 같다.

 

double EXP(const double x, const double limit) {
    double result = 1 + x;

    double x0 = x;
    int count = 1;
    while (true) {
        ++count;
        x0 = x0 * x / count;

        if (isinf(x0)) {
            break;
        }

        result += x0;

        if (fabs(x0) < limit) {
            break;
        }
    }

    return result;
}

double LN_e(double y) {
    double result = 0;

    if (y <= 0) {
        return INFINITY;
    }

    int N = 0;
    while (y >= 2) { ++N; y /= E; }
    while (y <= 0.4) { --N; y *= E; }

    const double x = (y - 1) / (y + 1);
    const double xx = x * x;

    double xxT1 = x;
    double xxT2;

    result = x;
    int i2 = 3;
    for (int i = 0; i < 20; ++i, i2 += 2) {
        xxT1 *= xx;
        xxT2 = xxT1 / i2;

        result += xxT2;
    }

    result = result + result + N;

    return result;
}

double POW(const double a, const double b, const double limit) {
    if ((fabs(a) < limit) && (fabs(b) < limit)) {
        return INFINITY;
    }

    if (fabs(a) < limit) {
        return 0;
    }

    if ((((1 - limit) < a) && (a < (1 + limit))) ||
        fabs(b) < limit) {
        return 1;
    }

    if (((1 - limit) < b) && (b < (1 + limit))) {
        return a;
    }

    return (EXP(b * LN_e(a), limit));
}