정삼각형 내부의 정삼각형의 면적은? 1/3

 

국내 최초, 세계 최강, 우주 최강 수학 팟캐스트 <적.콩.무>에 몇년 전에 나온 문제를 이제야 도전해봤다.

 

문제는 다음과 같다.

 

정삼각형의 각 꼭지점에서 마주보는 변의 \( \frac {1}{3} \) 지점에 선을 그어 만들어지는 정삼각형의 넓이는?

 

일단 문제를 그림으로 그려보면 아래와 같다.

여기서 바깥 정삼각형과 안쪽 파란색 정삼각형의 넓이의 비를 묻는 문제이다.

 

 

step1.

일단 파란색을 지운 뒤 최소한의 내용들만 그려보면 아래와 같다.

 

 

여기서 안쪽 삼각형의 꼭지점에서 마주보는 변과 평행한 직선을 그어 삼각형을 하나 그린다.

 

 

바깥쪽 삼각형을 \( \triangle ABC \) 라고 하고, 각 대변의 \( \frac {1}{3} \) 지점을 각각 \( D, E, F \) 라 부르기로 한다.

문제의 내부의 삼각형은 \( \triangle GHI \)라고 부르기로 한다.

그리고, \( G, H, I \)에서 그은 직선으로 만들어진 삼각형을 \( \triangle JKL \)이라고 부른다. 

 

 

여기서 \( \overline {AJ} \)의 연장선과 \( \overline {CF} \)의 연장선이 만나는 점을 \( M \)이라 부른다.

여기서 만들어지는 \( \triangle AIM \) 은 정삼각형인데...

 

이게 왜 정삼각형인지 설명을 못 하겠다^[각주:1]

 

여튼, \( \triangle AIM \)은 정삼각형이고, \( \triangle JHG,\triangle GHI,\triangle IHK,\triangle GIL \) 모두 합동인 정삼각형이다.

따라서, \( \triangle AJG\)도 \( \triangle GHI \)와 합동이다.

 

 

이에 따라 \( \overline {AG} \), \( \overline {BH} \), \( \overline {CI} \)와 \( \overline {GH} \)는 길이가 같다.

또한, \( O \)는 \( \overline {BD} \)의 중점이 되므로 \( \overline {BO} \)와 \( \overline {OD} \)와 \( \overline {DC} \)의 길이는 모두 같다.

 

step2.

위에서 그은 선들로 원래의 삼각형을 나눠서 보면 아래와 같은 영역으로 표현할 수 있다.

그럼 전체 면적 \( D \)는 아래와 같다.

 

\(S = 3a + 3b + 3c + 3d + e\)

 

 

또한, 이 영역들은 아래와 같이 정리할 수 있다.

 

\(\frac{2S}{3} = 2a + 2b + 2c + d + e \)

\(\frac{S}{3} = a + b + c + 2d \)

 

그리고, 이 두 식을 정리하면 다음과 같고,

 

\(e = 3d\)

 

이를 이용해 전체 면적 \( S \)를 조금 손보면 아래와 같다.

 

\(S = 3a + 3b + 3c + 6d\)

 

 

아래 그림에서는 다음과 같은 식을 도출할 수 있다.

 

\( 2a = b + c + d \)

 

이를 이용해서 S를 좀 더 정리하면 이렇다.

 

\(S = \frac{9}{2}(b+c)+\frac{15}{2}d\)

 

 

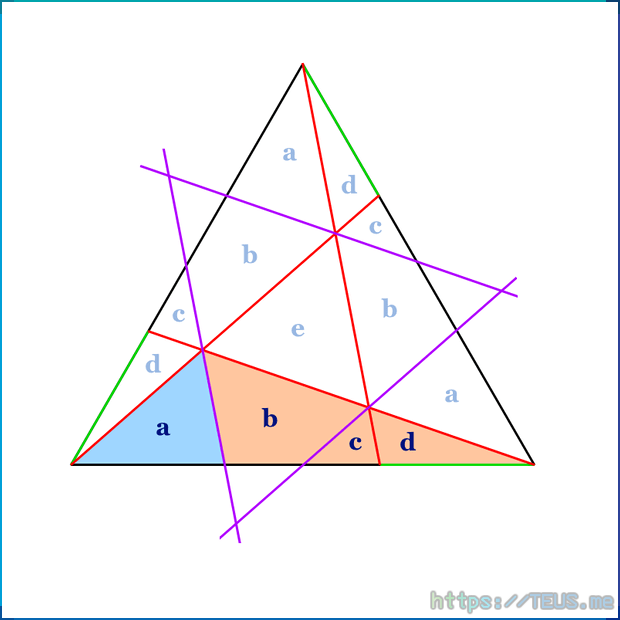
아래 그림에서는 또 다음의 식을 도출할 수 있다.

 

\( b + c = 3d \)

 

 

그럼 최종적으로 전체 면적 \( S \)는 다음과 같다.

 

\( S = 21 d \)

 

그런데, 위에서 \( e = 3d \) 라고 했으니, 전체 면적 \( S \)는 \( e \)의 7배가 된다.

 

 

1. 해석기하학으로 풀면 손쉽게 나오는 결론임 [본문으로]